研究概要
背景
1.MPCの機械系への適用
モデル予測制御は,有限評価区間の最適制御問題をオンライン計算で繰り返し解いてフィードバック制御入力を決定する手法である.多様な評価関数と制約条件に対する最適制御を実現する有効な制御法として知られ,制御周期が長いプロセス制御などに用いられてきた.従来は最適化の計算量が多いことが,制御周期が短い機械系に用いる際の障害となっていたが,近年の計算機の飛躍的な発達と計算アルゴリズムの高速化[2][3][4]により,機械系のリアルタイム制御への適用が可能になりつつある.
2.組込みCPUへの実装における問題点
機械系に対するMPCの適用例の多くは,クロック周波数が1GHz以上の高速な汎用CPUに実装している.しかし,実際の製品に広く用いられる組込みCPUは安価で信頼性が高く,豊富な入出力ポートなどを有する一方で,クロック周波数は数十MHz~数百MHzでCPUの計算処理速度が遅い上に,メモリ容量が小さく,回路実装された数学関数は限られる.さらに,頻繁に発生する外部割込みが最適化計算を中断するなど,計算リソースに厳しい制約がある.これらの理由から,組込みCPUへのMPCの実装は容易ではない.
3.組込みCPUを用いた脚車輪型移動ロボットの制御
一方で筆者らは,これまでに,移動ロボットを対象とした最適化計算の組込みCPUへの実装技術の確立を目指し研究を行ってきた[5].筆者が開発した図1の脚車輪型移動ロボット[6]は,クロック周波数が80MHzの組込みCPUを搭載し,3軸のSCARA型脚の変形により隘路通過と安定性確保の両立が可能である.筆者は過去に座標変換と部分的な陽解を用いて計算量を大幅に削減し,組込みCPU上で車輪配置のリアルタイム最適化計算を実現した[6].さらに,左右の車輪間距離(トレッド)のみを対象とするMPCを実装し,測域センサで検出した障害物の回避運動を低速走行で実現している[7].しかし,経路・姿勢・車輪位置(関節角)という多くの変数をMPCにより最適化し,高速走行するためには,組込みCPUに合わせた計算方法を確立する必要がある.

研究目標
本研究では,非線形ダイナミックスを有する脚車輪型移動ロボットの障害物回避と動力学走行制御の2つの非線形制御問題について,組込みCPUに実装したMPCでリアルタイム制御するための技術を確立することを目標とする.主な課題とその解決方法を表1にまとめる.図2に概略を示す.
| 組込みCPU実装上の課題 | 解決方法 |
|---|---|
| クロック周波数が低い | 非線形座標変換による部分線形化で処理速度を改善する.さらに部分的な陽解を用いて最適化計算の変数を削減し,計算速度を向上させる. |
| 数学関数の回路実装が乏しい | 高い計算精度が必要な最適化計算は,非線形座標変換で線形化した変数で厳密に数値計算する.この最適化計算の処理と,デジタル計測値や制御入力の間の非線形変換・逆変換は,高い計算精度は不要なので,ルックアップテーブルと補間による近似で高速計算する. |
| 割込みによるFPUレジスタの退避が発生し,最適化が中断する | 割込み処理は整数演算で記述し,割込みが発生しても最適化計算のFPUレジスタを退避せずにオーバヘッドを最小化する.フィルタ更新や制御入力計算などの浮動小数点演算は最適化計算の前後で纏めて実行する. |
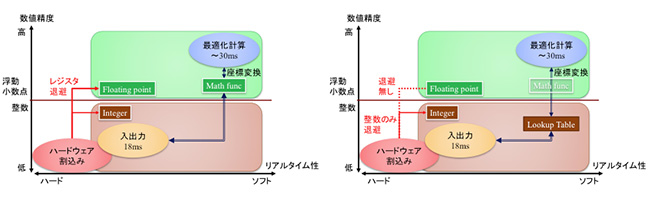
上記を図1の脚車輪型移動ロボットの組込みCPUに実装し,平成26年度までに下記2項目を実現する.これにより複雑な非線形系に対し,組込みCPUに実装したMPCが適用可能であることを実証できる.さらに,移動ロボットの障害物回避と運動制御に対するMPCによる効率的な計算方法を確立できる.
(a)障害物回避制御 測域センサの計測範囲を評価区間とした車体位置・方向と車輪位置の全状態に対するMPCを表1の方法を用いて高速計算し,実験でその有効性を検証する.
(b)動力学モデルによる走行制御 車輪の横滑り角を考慮した動力学モデルに基づく,MPCを実装する.これにより,前方の経路情報に基づいて車輪位置を変更し,タイヤ発生力配分制御を実現する.
研究計画・方法の概要
平成24年度は,表1の手法を用いた組込みCPU用MPCプログラムを製作する.また,従来の方法を用いた脚車輪型移動ロボットの障害物回避実験を行い,その限界と問題点を明らかにする.さらに,測域センサシステムと脚車輪型移動ロボットシステムを改良して信頼性を高める.平成25年度には脚車輪型移動ロボットの障害物回避制御に取り組み,評価関数の工夫によって,多様な障害物配置に対応できるMPC則を確立する.平成26年度には,車輪の横滑りを考慮した動力学モデルによる高速走行とタイヤ発生力配分制御を行い,提案する手法の性能を検証する.
研究成果
1.4輪独立操舵・駆動車両のMPC [h][l]
図3に示す4 輪を独立に操舵・駆動できる全方向移動車両は,狭隘な環境での運用に適している.一方で,車輪操舵の制約を考慮した制御が求められる.そこで,MPC により操舵の制約を陽に考慮した制御側を構築し,クロック周波数が80MHz のルネサスエレクトロニクス社製組込みCPUのSH7058Fに実装した.その結果,目標軌道追従性を保ちながら,操舵角度制限を考慮しない場合に発生した切返しを回避して連続な操舵角度を実現し[h],障害物回避に成功した[l].

2.非ホロノミック車両の障害物回避と車庫入れ [b][g][j][n]
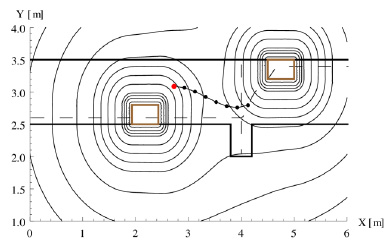
障害物回避や道幅により経路を制限された移動では,制約条件を陽に扱えるMPC は有効である.低速走行し車輪の横滑りを無視できる前輪操舵車の運動学は非ホロノミック系であるが,非線形MPCでは計算量が増加する.そこで,時間軸状態変換を適用してサブシステムに分解して線形化し,経路追従問題にMPCを適用した.その結果,組込みCPUのAMD Geode(クロック周波数は500MHz) でのリアルタイム制御[n]と,障害物回避を含んだ車庫入れ制御[b][g][j]を実現した.ポテンシャルを図4 に示す.
3.脚車輪型移動車両のMPC [f]
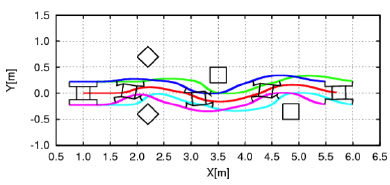
脚車輪型移動ロボットを対象として,関節角度を状態変数にとり,さらに角度の制約を陽に考慮したMPC則を導出し,障害物回避シミュレーション(図5)においてその有効性を検証した.予想通り制御性能は高いが計算コストが高いことを確認した.今後は前述の非線形変換などによる計算の効率化によって計算速度を向上させ,平成25年度以降の研究において,組込みCPUへの実装を目指す.
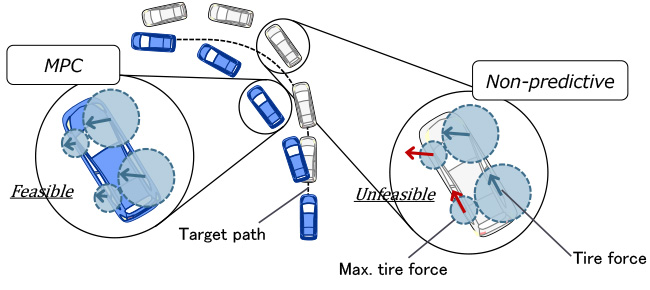
4.車輪の横滑りを考慮した運動の数値最適化・MPC [a][c][e][k]
移動ロボットに対する動力学モデルに基づくMPCを実現するための準備として,より簡単なモデルで記述される自動車型の車両において,車輪に横滑りを有するダイナミックスに対する非線形数値最適化による制御[k],MPC[e],ロバストMPC [a][c]を構築し,その有効性を検証した.(図6)
5.車両の自己位置推定 [i][m]
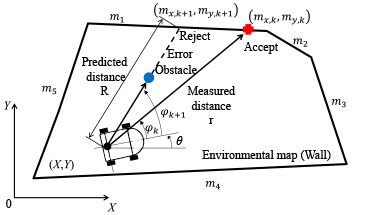
移動ロボットの誘導制御実験において,車両の位置・方向角の推定を高い精度で実現することは非常に重要である.そこで,レーザー測域センサによる周囲形状の計測結果を環境地図に対して数値最適化により適合させる手法を構築し[m],さらに改良したカルマンフィルタにより推定精度を向上させた[i].
参考文献
[2] Y. Wang and S. Boyd, “Fast model predictive control using online optimization”, IEEE Transactions on Control Systems Technology, Vol.18, No. 2, pp.267-278, 2010.
[3] M.N. Zeilinger, C.N. Jones, M. Morari, “Real-Time Suboptimal Model Predictive Control Using a Combination of Explicit MPC and Online Optimization”, IEEE Transactions on Automatic Control, Vol.56, Issue 7, pp.1524 – 1534, 2011.
[4] T. Ohtsuka, “A Continuation/GMRES Method for Fast Computation of Nonlinear Receding Horizon Control”, Automatica, Vol.40, No.4, pp. 563-574, 2004.
[5] 2009~2011年度 科学研究費補助金 基盤研究(C),脚車輪型移動ロボットの最適脚配置に関する研究(課題番号21560475),野中 謙一郎,2009~2011.
[6] Kenichiro Nonaka, Nonlinear Tracking Control and Leg Optimal Allocation for Wheeled Mobile Robots with 3DOF SCARA Legs, 9th Int. Conf. on Motion and Vibration Control, 2008.
[7] 大川 功,野中 謙一郎,経路の道幅を考慮した脚車輪型ロボット車輪位置のモデル予測制御,計測自動制御学会産業論文,10巻23号,pp.190-197,2011.
[8] 栗島佑典,野中謙一郎,反復数値計算によるSMCを用いた前輪操舵車の非線形ロバスト操舵駆動統合制御,日本機械学会論文集C編,77巻782号,pp.3705-3720,2011.
[9] Naoki Takahashi, Kenichiro Nonaka, Model Predictive Obstacle Avoidance and Wheel Allocation Control of Mobile Robots Using Embedded CPU,Journal of System Design and Dynamics, Vol.6, No.4, pp. 447-465,2012.
[10] 野中謙一郎,渡辺陽平,キャスタ型オドメータと非線形オブザーバを用いた移動ロボットの速度推定,日本機械学会論文集(C編), 78巻791号,pp.155-171,2012.
研究成果
[a]Kenichiro Nonaka, Takatsugu Oda, “Model Predictive Sliding Mode Control for Four Wheel Steering and Driving Vehicles”, Proceedings of 7th IFAC Symposium on Advances in Automotive Control, pp.784-789, 2013/9
[b]Kentaro Oyama, Kenichiro Nonaka, “Model Predictive Parking Control for Nonholonomic Vehicles Using Time-State Control Form”, Proceedings of European Control Conference 2013, pp.458-465, 2013/7
[c]小田貴嗣, 野中謙一郎, “モデル予測制御とスライディングモード制御による小型電気自動車の最適ロバスト制御”, 自動車技術会春季大会予稿集, 発表番号244, 2013/05
[d]野中謙一郎, “車両型移動体への実時間最適制御の実装”, 第13回制御部門大会(チュートリアルセッション:移動体の誘導制御における実時間最適化・最適制御), 2013/03.
[e]小田貴嗣, 野中謙一郎, “キャンバ角制御を考慮した小型四輪操舵駆動電気自動車のモデル予測制御”, 第13回制御部門大会, 発表番号PS-001, 2013/03.
[f]Naoki Takahashi, Kenichiro Nonaka, “Model Predictive Obstacle Avoidance Control for Leg/Wheel Mobile Robots with Optimized Articulated Leg Configuration”, 51st IEEE Conference on Decision and Control, pp.1782-1789, 2012/12.
[g]小山健太郎, 野中謙一郎, “障害物が存在する環境下におけるモデル予測車庫入れ制御”, 第13 回計測自動制御学会システムインテグレーション部門講演会概要集, pp.2111-2114, 2012/12.
[h]高橋直樹, 野中謙一郎, “操舵角の制約を陽に考慮した全方向移動ロボットのモデル予測経路追従制御”, 第13 回計測自動制御学会システムインテグレーション部門講演会概要集, pp.2107-2110, 2012/12.
[i]廣町悠太郎, 野中謙一郎, “環境形状を考慮したLRF計測とオドメトリのEKF融合による車両の自己位置推定”, 第55回自動制御連合講演会, pp.1356-1359, 2012/11.
[j]小山健太郎, 野中謙一郎, “切り返し動作を有する非ホロノミック車両の時間軸状態制御形を用いたモデル予測制御”,第41回制御理論シンポジウム資料 , pp.79-84, 2012/09.
[k]細谷知之, 野中謙一郎, “超平面への拘束を考慮した非線形観測器とスライディングモードによる車両制御実験”, 第41回制御理論シンポジウム資料, pp.55-62, 2012/09.
[l]高橋直樹, 野中謙一郎, “局所停留点を考慮した移動ロボットのモデル予測障害物回避制御”, Dynamics and Design Conference 2012, 10頁, 2012/09.
[m]廣町悠太郎, 野中謙一郎, “LRFとデッドレコニングの融合による車両の自己位置推定”, 第29回誘導制御シンポジウム, pp.31-38, 2012/05.
[n]小山健太郎, 野中謙一郎, “経路制約を考慮した非ホロノミック車両のためのモデル予測制御”, 第29回誘導制御シンポジウム, pp.65-72, 2012/05