1.緒言
ハニカムコアサンドイッチパネルは蜂の巣状のコア材を上下から表面板となる二枚の平板で挟み,接合した複合構造材料である.ハニカムコアサンドイッチパネルは容積の95%以上が空気で構成されているために軽量で,コア材の座屈による衝撃緩衝効果に優れており,特にパネル全体に一様な荷重が作用する場合に強い.一方,落錘衝撃など局部的な荷重に対しては表面板の作用点近傍とその直下のコア材だけで支えるため,パネルの力学特性にはコア材に加え,表面板の機械的性質が大きく影響する.この場合のパネルの力学的挙動の解明は十分とはいえず,パネルの力学特性は実験的に取得しているのが現状である[1, 2].そこで,本研究では,ハニカムコアサンドイッチパネルに対して,より汎用性のある設計指針を確立するため,局部荷重が作用する際のパネルの力学特性を理論的に得る力学モデルの構築を目的として,ハニカムコアサンドイッチパネルによる静的局部圧縮試験と有限要素解析を中心に研究を進めた.

2.静的局部圧縮試験による実験値の取得
試験片にはコア材のセルサイズSを8.7mmまたは17.3mmとしたアルミニウム製ハニカムコアサンドイッチパネルを用いた.
静的局部圧縮試験では,図1に示すように試験片を底面固定した後,半径30mmの半球状の圧子を試験片の中央部に対して押込んだ.以下,本研究では圧子と接触するほうの表面板を上表面板と呼称する.試験の際,圧子に作用する荷重を取得するとともに,上表面板に生じるたわみとひずみの測定を行った.図2にひずみ測定試験に用いた試験片の試験後の写真を示す.図より,試験片の中央部は圧子先端の形状に押しつぶされ,凹みが形成されたことがわかる.上表面板に形成された凹みの外周部はコア材のうち,圧潰しなかったセル壁が支持点になる形で折れ曲がっていた.これらのことから,コア材のセル壁はその直上の上表面板が圧子によって押込み変形する際の支持点になったと考えられる.また,試験片の観察から上表面板に生じたたわみは試験片の中央を中心軸としてほぼ軸対称状であること,および,ひずみの測定値から上表面板の面内変形はねじりを伴わないことが確認された.図3に各試験から得られた荷重変位線図を示す.図中に示したすべての荷重変位線図における荷重のピークは,試験中に上表面板にき裂が入ったことで生じたことが確認された.これまでの研究[2]から,荷重のピーク値はき裂の発生位置に依存することがわかっている.また,図より,コア材のセルサイズの小さいほうが荷重変位線図のピークに至るまでの傾き(以下,変形抵抗と呼称する)が大きいことがわかった.

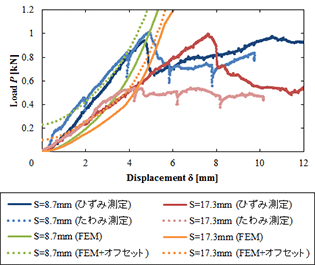
3.有限要素解析による力学モデルの構築
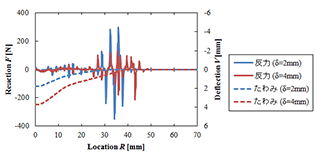
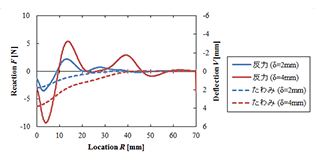
静的局部圧縮試験の結果を考慮して,解析モデルとして上表面板を直径140mmの円板で近似し,軸対称要素で離散化した有限要素モデルを用いた.境界条件として,たわみ測定試験から得られた上表面板のたわみ曲線を強制変位で与え,ひずみ増分理論にもとづく弾塑性有限要素解析を行った.図4に推定された上表面板の反力分布の一例を示す.図より,反力分布の推定結果は振動していることがわかる.そこで,逆解析手法を援用し,数値解の正則化コードを組込んだ有限要素解析プログラムを新たに開発した.これにより得られた反力分布の推定結果を図5に示す.図より,数値解の正則化によって,図4よりも滑らかな反力分布が得られたことがわかる.図中において,原点近傍の鉛直下向きの反力分布は圧子によるものと考えられる.すなわち,この反力分布の合力が荷重変位線図の荷重値になる.また,原点に配した節点の鉛直下方向の変位が圧子の変位に等しいと考えられるので,この変位に対して,反力分布の推定結果から得られた荷重値をプロットしたものを図3に示した.図より,本有限要素解析から得られた荷重変位関係のオーダーは,荷重のピークが現れるまでの実験値とよく合うことがわかる.特に,変位2mmから4mmの間において,変形抵抗の計算値と実験値はほぼ一致した.なお,図5において,原点近傍の鉛直下向きの反力分布のちょうど外側,すなわち位置R=10mmからモデルの外周にかけてみられる鉛直上向きの反力分布はコア材の支持反力に相当すると考えられる.これらの反力分布について,その最大値を位置R,要素分割幅,円周率の積で除した値は,変位2mmのときで約0.2MPa,変位4mmのときで約0.4MPa であった.これらの値はハニカムコアサンドイッチパネルの全面圧縮時のプラトー領域における公称応力[3]のオーダーに近いことが確認された.今後,コア材の支持反力に関するさらなる詳細な解析手法およびその妥当性について,引き続き検討を加える予定である.
4.結言
本研究では局部荷重を受けるハニカムコアサンドイッチパネルの力学モデルの構築を目的として,静的局部圧縮試験と有限要素解析を行い,以下の結論を得た.(1)静的局部圧縮試験の結果から,上表面板に生じる変形は面内ねじりを伴わない軸対称問題としてモデル化できることがわかった.(2) 逆解析手法を援用し,数値解の正則化コードを組込んだ有限要素解析プログラムを新たに開発した.本解析プログラムによって得られた荷重変位関係は,荷重のピークが現れるまでの実験値とよく合うことが確認された.
参考文献
Vol. 43, No. 6 (2006), pp. 1746-1763.
[2] 岸本喜直ほか, 日本機械学会論文集A編, Vol.79, No.808 (2013), pp.1752-1767.
[3] 小林志好ほか, 日本機械学会論文集A編, Vol.76, No.771 (2010) , pp.1429-1435.
本研究に関連する成果発表
(2)岸本喜直, 小林志好, 大塚年久, 山縣森,変形形状データを利用した逆解析によるサンドイッチ板の支持反力
分布推定法,日本機械学会材料力学部門若手シンポジウム2015, 2015年8月(発表予定).
(3)Y. Kishimoto, Y. Kobayashi, T. Ohtsuka, R. Hanashima, Study on mechanical characteristics of double layer honeycomb core sandwich panel subjected to drop weight impact, The Fourth Asian Conference on Mechanics of Functional Materials and Structures, 2014年10月.
(4)Y. Kobayashi, Y. Kishimoto, T. Ohtsuka, Effect of core positioned in circumferential direction on drop weight impact, The Fourth Asian Conference on Mechanics of Functional Materials and Structures, 2014年10月.
(5)唐津瑛, 小林志好, 岸本喜直, 大塚年久, CFRPを表面板に用いたハニカムコアサンドイッチパネルの局部圧
縮疲労特性に関する研究, 日本機械学会2014年度年次大会, 2014年9月.