研究概要
アクチュエータが故障した劣駆動状態の衛星システムに対し,可制御性解析,平衡点解析をおこなうことで,2つまたは1つのリアクションホイールを使ってどのような姿勢が実現可能かを明らかにし,実現可能な姿勢を安定化する制御則をそれぞれ提案した.さらに故障時に静止した姿勢でアンテナを向ける事ができる領域を最大にすることを見据えた最適なアンテナ配置を提案した.
背景
2010年10月姿勢制御に関するトラブルを含め様々な困難に見舞われながらも小惑星探査機「はやぶさ」(MUSES-C) が地球に帰還.昨年には太陽系外惑星探査宇宙望遠鏡「ケプラー」が姿勢制御用アクチュエータのトラブルのためミッションを終了した.宇宙空間を飛行する衛星システムにとって姿勢制御は最重要な機能の一つであり,アクチュエータの故障により姿勢制御が不能になるとミッション継続は不可能となる.このような理由からアクチュエータ故障に見舞われた衛星システムの姿勢ダイナミクスに対する安定性解析,制御系構築がフェイルセーフの観点から求められている.
研究の目的
衛星システムの高精度な姿勢制御にはリアクションホイールというホイールを回転させた反作用で姿勢を制御するアクチュエータが用いられる.本研究ではアクチュエータ故障によってFig. 1 に示すようなリアクションホイールの数が姿勢表現の自由度よりも少なくなってしまった劣駆動状態の衛星システムを対象とし,どのような運動が,特に通信や観測に必要なアンテナを目的の方向へ向けるという意味で,どのような運動や姿勢が実現可能かを可制御性解析,平衡点解析を通して明らかにし,実現可能な運動の中で自由に姿勢を制御するための姿勢制御手法を確立することを目的とする.
研究成果
衛星システムの姿勢はロール,ピッチ,ヨー角で代表されるように3次の自由度を持つ.このため劣駆動状態の衛星システムとしてリアクションホイールが2つ,または1つの場合を分けて考える必要がある.
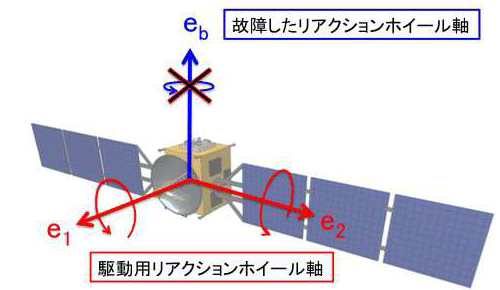
1.2台のリアクションホイールが利用できる場合 [1-3,5]
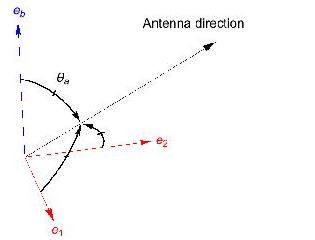
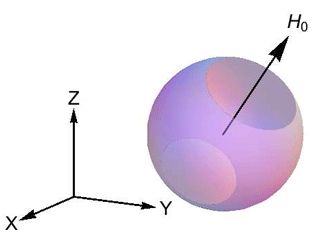
この平衡点解析より,衛星設計の段階でアンテナ配置を工夫することでリアクションホイールが故障した場合にアンテナを安定的に向けることができる領域を最大化することができる.一般に,どの軸のリアクションホイールが故障するかは衛星の設計段階ではわからないことから,アンテナを安定的に向けることができる領域を最大化するアンテナ配置として,任意のリアクションホイール軸とアンテナ軸のなす角を最大にしたFig. 2 に示すアンテナ配置を提案した.Fig. 1 ではアンテナがe1 軸に取り付けられているが,提案するアンテナ配置では,任意の軸から等角度(θa = cos-1(1/√3)) になっている.提案するアンテナ配置を持つ衛星システムがアクチュエータ故障で2つのリアクションホイールになった場合アンテナを向けることができる領域は,故障したリアクションホイール軸によらず,Fig. 3 に示す初期角運動量ベクトル周りに対称な球面上の領域となる.
静止姿勢を安定化する制御則
この安定化問題は非ホロノミック系の制御問題に分類され,時不変連続な状態フィードバックでは漸近安定化することができないことが知られている.このような姿勢制御問題に対して,姿勢表現の一つであるロドリゲスパラメータを,固定の比を保ちながら発散させると対応した一つの姿勢に収束するという性質に着目し,制御則を構築した.この制御則によって静止可能な任意の姿勢を安定化することを可能にした[1-3,5].
アンテナ軸の向きを安定化する制御則
アンテナを用いた通信や観測だけを考えるとアンテナ軸まわりの回転は無視することができる.任意の姿勢は回転軸を表す単位ベクトルと回転量を表すスカラー量を用いて表現できる.アンテナ軸の向きを安定化するためには姿勢の回転軸を表す単位ベクトルがアンテナ軸と一致すればよい.これを実現するために入出力線形化と呼ばれる手法を回転軸を表す状態量に対し適用する制御則を提案し,数値シミュレーションでその有効性を確認した[3].
2.リアクションホイールが1 台のみ利用可能な場合 [4]
初期角運動量が存在しない場合,角運動量が保存するのでリアクションホイールでの回転自由度しか存在しない.初期角運動量が存在する場合,初期角運動量とリアクションホイールの入力の非線形な相互作用によって,取りうる姿勢は自明ではない.このような非線形性の強いシステムに対し可制御性の解析を行い,不可制御となる条件はリアクションホイール軸と慣性主軸,初期角運動量ベクトルが全て一致する場合のみであることを明らかにした.この解析から周期的な姿勢制御しかできないことがわかり,アンテナを周期的に目標の向きへ向ける制御則を提案した.
発表論文
[1] 関口和真 : 2 リアクションホイールを用いたスペースクラフトの目標平衡点の安定化制御 ; 第 1 回制御部門マルチシンポジウム , 5G5-2 (2014).
[2] 勝山裕輝 , 関口和真 , 三平満司 : 時間軸状態制御形を用いた 2 ホイール衛星の姿勢制御 ; 第 57 回システム制御情報学会研究発表講演会 , 133-4 (2013).
[3] Y. Katsuyama, K. Sekiguchi, M. Sampei: Spacecraft attitude control by 2 wheels with intial angular momentum; Proceedings ofSICE Annual Conference 2013, 1890-1895 (2013).
[4] K. Tahara, K. Sekiguchi, M. Sampei: Controllability Analysis and Periodical Antenna Pointing Attitude Control of a Single Rotor Spacecraft; Proceedings of SICE Annual Conference 2013, 1580-1585 (2013).
[5] 勝山裕輝 , 関口和真 , 三平満司 : 初期角運動量を有する宇宙機のホイール故障時における劣駆動姿勢制御 ; 日本機械学会第13回「運動と振動の制御」シンポジウム , (2013)